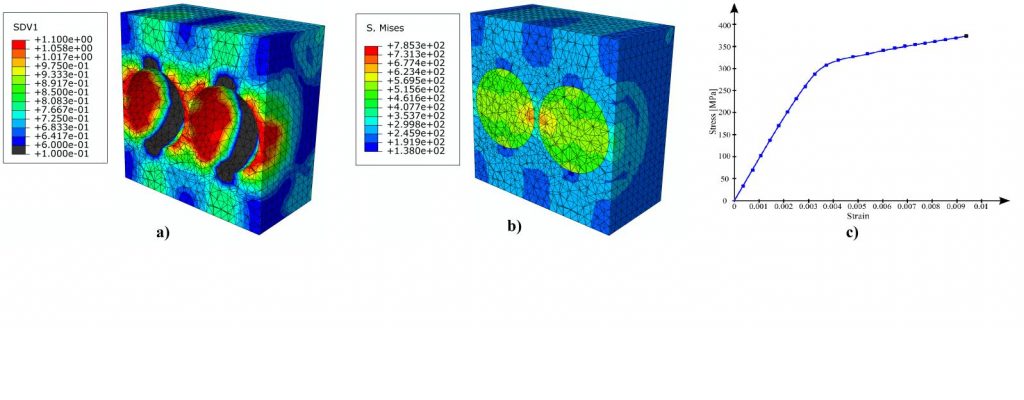
Summary: A composite may be defined as a multi-phase material in which the phase distribution and geometry have been controlled in order to optimize one or more properties. Compared with traditional materials, composites have various desirable advantages, such as high strength-to-weight and stiffness-to-weight ratio and excellent wear and corrosion resistance, etc. Among them, Metal Matrix Composites (MMCs) reinforced with ceramic particles, are undergoing rapid development to keep up with the requirements of aerospace and automotive industry applications where minimal weight, and increased efficiency are critical. Modelling and prediction of the overall elasto-plastic response and local damage of Particle Reinforced Metal Matrix Composites (PRMMCs) require a thorough understanding of the microstructural complexities. Indeed, the inhomogeneous spatial distribution of the particles, their irregular morphology, the effect of matrix/particles interface as well as the constituent’s material parameters strongly influence the heterogeneous material behaviour. This research is based on the effect of both particles spatial distributions and particles fraction volumes on the heterogeneous elasto-plastic behaviour of PRMMCs by means of optimization techniques. The numerical upper bound and lower bound of the elastic module along the x direction have been calculated for different numbers of particles (1, 2, 3, 4, 5, 6, and 8) and particle fraction volumes (5%, 10%, 15% and 20%). A composite modelling framework, developed at University of Strathclyde has been employed throughout the numerical simulations. This comprises Python, Matlab and FORTRAN codes, including the Representative Volume Element (RVE) generator, Adaptive Periodic Boundary Conditions (APBC) code, Homogenization code, and Damage code. The finite element method is applied to solve the boundary value problem. In particular, the finite element software package, Abaqus has been used, coupled with Matlab Genetic Algorithm and the composite modelling framework.
Timeframe: September 2016 – February 2017
People: Dario Giugliano, Lorenzo Gentile, Haofeng Chen, Edmondo Minisci
Partners: Politecnico of Torino