Summary: In the literature on uncertainty propagation, intrusive approaches are methods that require a modification of either the system model or operators used to evaluate the quantities of interest. On the other hand non-intrusive approaches build a representation of the quantity of interest or of its probability distribution from a set of samples. Non-intrusive approaches, therefore, take the system through which uncertainty is propagated as a black
box. While in the literature on uncertainty propagation in computational fluid dynamics non-intrusive schemes, mainly based on Polynomial Chaos Expansions, have become more popular than their intrusive counterpart, in orbital mechanics the use of Taylor polynomial algebra has gained popularity as a valid alternative to direct Monte Carlo simulations. Taylor polynomial algebra starts from variationals of the uncertain quantities with respect to a nominal value. Variationals initially describe a hypercube in the uncertain space, with uncorrelated variables, that is mapped into a gen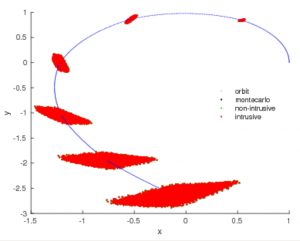
erally non-convex region through the dynamical model. The propagation is performed by introducing an algebra, on Taylor polynomials, that replaces the standard computer algebra on real numbers. This technique is based on the so called Truncated Power Series Algebra (TPSA) introduced by Berz in 1986 and extended to rigorous numerics in 1997 with the introduction of Taylor Models. Numerical integration and evaluation of the dynamics are performed in the TPSA, hence at each integration time-step the full polynomial representation of the current state is available. The same idea can be generalised to a different set of basis functions providing that the corresponding algebraic rules between monomials can be defined. The idea of a more generic TPSA dates back at 1982 with the name of Ultra Arithmetic. However, in 2003 the possibility of using a TPSA alternative to the one built on Taylor basis was discarded because of several drawback related to polynomial multiplications and growth of the magnitude of the coefficients. It was with the work of Brisebarre and Joldes in 2010 that a formal comparison of the TPSA with Taylor, Tchebycheff and Newton basis was given. The results proved, for the univariate case, that the interpolation polynomials constructed in the Tchebycheff and Newton basis algebrae were able to achieve smaller reminders than Taylor models, requiring nevertheless more computing time, for the same order of expansion.
One of the main advantages of using Tchebycheff series expansions is the uniform convergence over the interval of expansion, that guarantees near-minimax approximation. The complexity and accuracy of the proposed Generalised Polynomial Algebra (GPA), its generalisation to the multivariate case, and the comparison to its non intrusive counterpart is under investigation in this current research project.
References:
Riccardi, A., Tardioli, C., Vasile, M., “An intrusive approach to uncertainty propagation in orbital mechanics based on Tchebycheff polynomial algebra”, 13 Aug 2015, Proceedings AAS/AIAA Astrodynamics Specialist Conference, ASC 2015.
Ortega Absil C., Serra R., Riccardi A., Vasile M. “De-Orbiting and Re-entry Analysis with Generalised Intrusive Polynomial Expansions”, Proceedings of the 67th International Astronautical Congress, Guadalajara, Messico 2016.
Timeframe: January 2015 – ongoing
People: Annalisa Riccardi, Carlos Ortega Absil, Massimiliano Vasile, Romain Serra